Gegeben seien die m Datenpunkte
Gesucht ist ein offener Basis-Spline mit n+1 Polygonecken,
bestehend aus quadratischen Polynomen (Ordnung 3), der diese
Datenpunkte approximiert. Der Knotenvektor soll uniform sein und wie
folgt aussehen 
:
Jedem Datenpunkt 
, 
ordnet man einen Parameter 
zu, bei dem sich der Spline 
möglichst nahe an
annähern soll. Um eine gleichmäßiges Durchlaufen der
Kurve mit dem Parameter zu erreichen, wählt man den Parameter
eines Datenpunktes entsprechend seines Abstandes auf der Kurve zum
Ausgangspunkt. Eine sinnvolle Annäherung diese Abstandes liefert
die Länge des Polygonzuges über die Datenpunkte. Für
den Parameterbereich 
ergibt das:
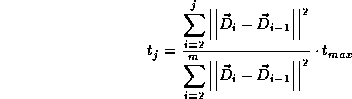
Ein Standardverfahren zur Approximation ist die Methode der
kleinsten Fehlerquadrate, das hier eine Minimierung der quadratischen
Abstände zwischen den Datenpunkten
und den ihnen zugeorndeten Punkten
auf dem Spline bedeutet. Man betrachte daher als zu minimierende
Summe:
Sie ist eine Funktion der zu bestimmenden Polygonpunkte 
, 
, 
, 
. Für deren voneinander unabhängigen Koordinaten 
und 
, 
ergeben sich aus der notwendigen Bedingung für ein Minimum von
S die linearen Gleichungssysteme:
Im folgenden werden nur noch die x-Koordinaten betrachtet. Die Bestimmung der y-Koordinaten der Polygonecken verläuft dann analog.
Die x-Koordinatenfunktion des Splines ist nach Definition gegeben durch
Die partielle Ableitung von 
nach
ist offenbar
Aus dem Gleichungssystem ergibt sich damit
:
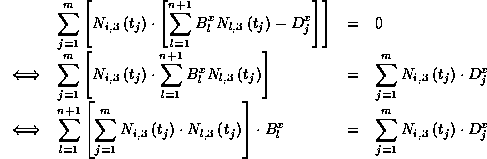
Diese etwas unübersichtliche Schreibweise läßt sich durch Einfürung folgender Matrizen deutlich vereinfachen:
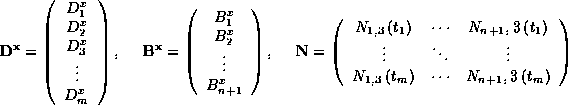
Durch sukzessives Ausführen der Matrizenmultiplikation läßt sich zeigen, daß die folgende Gleichung in Matrizenschreibweise äquivalent zum Gleichungssystem oben ist:
Die Einträge der Matrix 
können mit den
bestimmt werden. Der Gaußsche Algorithmus liefert dann die
gesuchten x-Koordinaten der Polygonecken, die sich mit
Matrizeninvertierung auch wie folgt darstellen lassen:
